SPN密码

以一个简单的SPN密码为例：

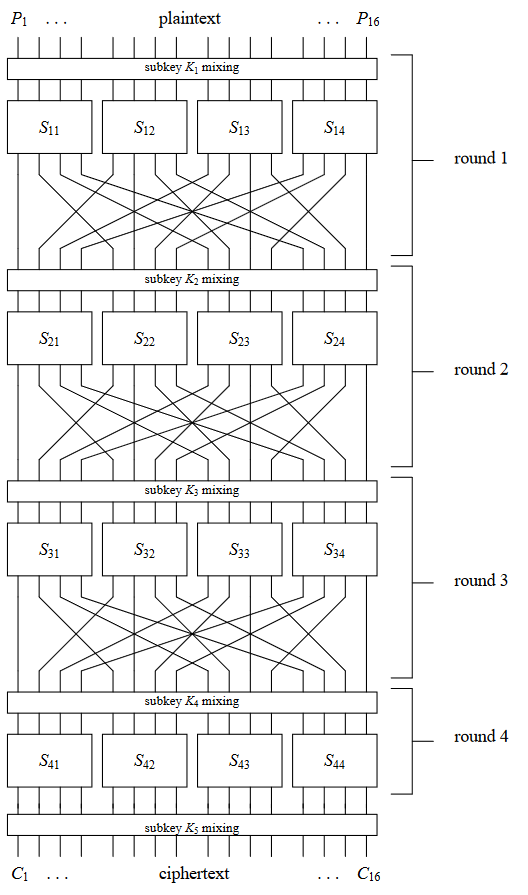
每条连线都表示1位，明文块大小为16位，S盒大小为4位。该密码主要由三部分组成：

1. S盒都是一样的，它们作如下的映射：
   
2. S盒之后，所有的位参与一次排列，将原本在i位置的位换到\text{output}[i]上。排列的具体位置如下：
   
3. 密钥混淆就是简单的异或操作。
   我们关心的问题是线性分析，因此为了简化该密码，我们认为每个子密钥都是独立随机生成的，而非由密钥生成算法产生的。

线性函数和仿射函数

在\mathbb R上，线性函数是形如y=ax的函数，而形如y=ax+b的函数叫做仿射函数。仿射函数能够表达平移，而线性函数不能。
y=Ax, A\in M_{2\times 2},x\in \mathrm R^2也是一个线性函数，它能够表达一个二维平面上的线性变换，例如

 A=
\left[\begin{array}{l}
\cos \alpha & -\sin\alpha \\
\sin\alpha & \cos \alpha
\end{array}
\right]

表示逆时针旋转\alpha。

## 位移的角度
a = pi / 6
m = matrix([[cos(a), -sin(a)], [sin(a), cos(a)]])
## 形成长方形的四个点
points = [[0, 0], [1, 0], [1, 3], [0, 3]]
## 变换后的四个点
new_points = [m * vector(p) for p in points]
## 绘制原图形
rect1 = polygon(points, alpha=0.5, rgbcolor=(1/8,3/4,1/2))
## 绘制新图形
rect2 = polygon(new_points, alpha=0.5, rgbcolor=((1/8,1/4,1/2)))
(rect1 + rect2).plot().save("example.png")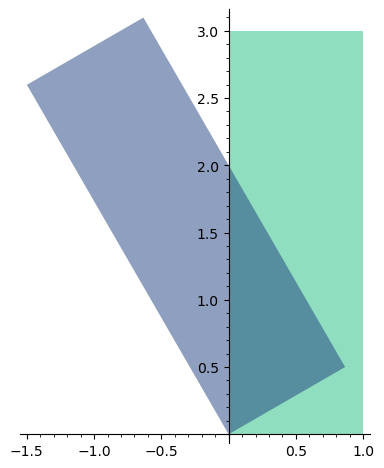

这样的线性变换只能进行旋转、拉伸操作，无法进行平移，而仿射变换y=Ax+b,b\in\mathbb R^2则提供了平移的能力，可以将图形向b向量所示的方向平移。

同样地，在F_2^n中，我们将\bigoplus_{i\in F_2} X_i=0称为线性函数，而\bigoplus_{i\in F_2} X_i=1叫做仿射函数。

线性分析

1. 思路

线性分析是一种已知明文攻击，即已知一组明文-密文对的情况下进行攻击（攻击者不能自由选择明文并加密）。线性分析试图使用线性（或）仿射关系来模拟明文位和密文位之间关系（也就是，试图用线性的东西来替换掉密码中的非线性部分）。例如，在S盒的两端：

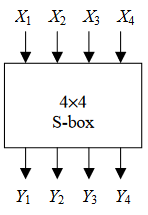
由于S盒是已知的，那么某个线性表达式，如X_2\oplus X_3\oplus Y_1\oplus Y_3\oplus Y_4=0，在所有的输入组合中，成立的概率是能够计算出来的，上式成立的概率为3/4。
不难看出，如果一个线性表达式成立的概率为p，那么其对应的仿射表达式成立的概率为1-p。因此，如果一个线性表达式成立的概率很低，我们只要取用对应的仿射表达式即可。因此我们真正关心的指标不是某个线性表达式成立的概率，而是其与\frac 12之间的偏置值，定义为|p-\frac 12|。

2. 堆积引理

如果X_1,X_2\in F_2，且有如下概率分布：

\Pr(X_1=i)= \left\{
\begin{aligned}
p_1 & ,i=0 \\
1-p_1 & ,i=1
\end{aligned}
\right.\\
\text{}\\
\Pr(X_2=i)= \left\{
\begin{aligned}
p_2 & ,i=0 \\
1-p_2 & ,i=1
\end{aligned}
\right.

那么不难得到，线性表达式X_1\oplus X_2=0成立的概率为：

\begin{aligned}
&\Pr(X_1\oplus X_2=0)\\
=&p_1p_2+(1-p_1)(1-p_2)\\
=&(\frac12+\epsilon_1)(\frac12+\epsilon_2)+(\frac12-\epsilon_1)(\frac12-\epsilon_2)\\
=&\frac12+2\epsilon_1\epsilon_2
\end{aligned}

其中\epsilon_i表示对应变量的偏置值。推广到n个变量，可以得到如下引理：
堆积引理 假设有n个独立的布尔变量X_i，那么

\Pr(\bigoplus_{i\in\mathbb Z_n} X_i=0)=\frac12 + 2^{n-1}\prod_{i=1}^{n}\epsilon_i

由堆积引理可以看出，如果我们有多个线程表达式要组合在一起，并求成立的概率，那么它们的偏置值的符号并不重要，因为无论怎么组合，最终仅影响上式第二项的符号，也就是说，最后得到的线性表达式的偏置值的绝对值是不会被影响的。

3. 分析S盒

我们研究的密码中，仅有S盒为非线性部分，因此主要来分析它。
本例中S盒的输入和输出是4位，因此仅有2^8=256个不同的线性表达式，而通过上面的分析，我们不用考虑仿射表达式（1减去对应的线性表达式的概率即可），而对于每个线性表达式，我们需枚举2^4=16种输入，即可得到所有线性表达式（及仿射表达式）成立的概率（或者说，偏置值）。
这里以线性表达式X_2\oplus X_3\oplus X_4\oplus Y_1\oplus Y_4=0为例，枚举所有的可能输入值，计算成立的次数：

using BIT4 = uint8_t;
// 遍历4位变量x，循环体为body
#define FOR_4(x, body) for (BIT4 x = 0x00; x <= 0x0f; x++) { body; }

int count = 0;
    BIT4 X = 0b0111;
    BIT4 Y = 0b1101;
    FOR_4(in, {
        BIT4 out = sbox[in];
        // in和out分别为sbox的输入和输出，与XY分别做与操作
        // 表明我们仅关心XY中为1的部分
        BIT4 nx = in  & X;
        BIT4 ny = out & Y;
        // 共有偶数个1，即为线性表达式成立
        if ((CountOne<4>(nx) + CountOne<4>(ny)) % 2 == 0) {
            count++;
        }
    })
    cout << "Linear expression: X = " << bitset<4>(X) << ", Y = " << bitset<4>(Y) << ". ";
    cout << "P = " << count << " / 16, ";
    cout << "Bias = " << count - 8 << endl;

// output ==> Linear expression: X = 0111, Y = 1101. P = 10 / 16, Bias = 2

采用这种方法，我们可以计算出所有线性表达式成立的概率，见附件1。

FOR_4(X, {
    FOR_4(Y, {
        int count = 0;
        FOR_4(in, {
            BIT4 out = sbox[in];
            BIT4 nx = in  & X;
            BIT4 ny = out & Y;
            if ((CountOne<4>(nx) + CountOne<4>(ny)) % 2 == 0) {
                count++;
            }
        })
        PrintResult(X, Y, count);
    })
})

4. 分析整个密码结构

前R-1轮的线性拟合

为了表示比较方便地表示中间变量，如图所示，我们定义U_i,V_i分别表示第i轮的S盒的输入和输出。

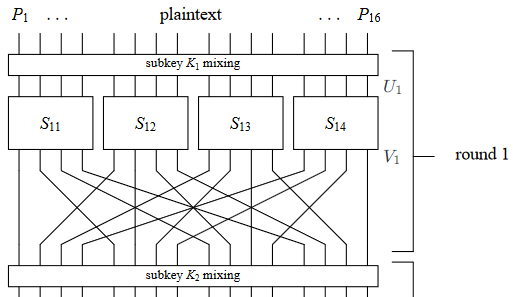
一个明文块16位，我们选择某些位，然后利用我们已经得到的线性表达式一直计算到密文（这个过程中将密钥K_i作为已知参数），最终得到有关P,C,K的线性表达式，而其成立的概率可由堆积引理计算得到。

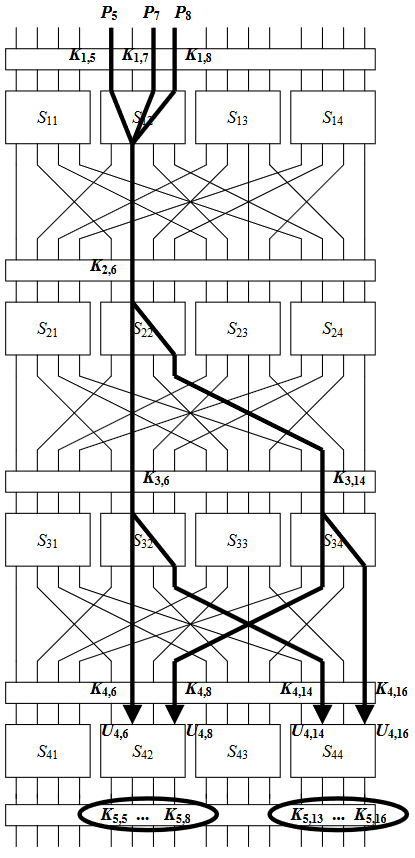
举例，参考如上图所示的路线，我们选择P_5,P_7,P_8作为输入位，这几位仅与S_{12}有关，对于S_{12}，我们选用线性表达式X_1\oplus X_3\oplus X_4=Y_2作为线性拟合。根据之前的结果，该线性表达式成立的概率为12/16，偏置为1/4。
将上面表达式中的X,Y用上面定义的符号表示，可得：

 P_5\oplus K_{1,5}\oplus P_7\oplus K_{1,7}\oplus P_8 \oplus K_{1,8}=V_{1,6} 

对于第二轮，我们选择X_2=Y_2\oplus Y_4，成立的概率为4/16，偏置值为-1/4。按照相同的方法，我们可以得到：

\begin{aligned}
U_{2,6}&=V_{2,6}\oplus V_{2,8}\\

V_{1,6}\oplus K_{2,6}&=V_{2,6}\oplus V_{2,8}
\end{aligned}

将这两个表达式连接在一起，可得：

 V_{2,6}\oplus V_{2,8}\oplus P_5\oplus P_7\oplus P_8\oplus K_{1,5}\oplus K_{1,7} \oplus K_{1,8}\oplus K_{2,6}=0 

根据堆积引理，该式成立的概率为\epsilon=\frac 12+2\times (-\frac 14)\times \frac14=\frac 38。
同样地，我们计算R-1轮，还能得到以下一系列表达式：

\left\{
\begin{aligned}
L_1:& P_5\oplus K_{1,5}\oplus P_7\oplus K_{1,7}\oplus P_8 \oplus K_{1,8}\oplus V_{1,6}=0 \quad &&,\epsilon_1=\frac14\\
L_2:& V_{1,6}\oplus K_{2,6}\oplus V_{2,6}\oplus V_{2,8}=0 &&,\epsilon_2=-\frac14\\
L_3:& V_{2,6}\oplus K_{3,6}\oplus V_{3, 6}\oplus V_{3,8}=0 &&,\epsilon_3=-\frac14\\
L_4:& V_{2,8}\oplus K_{3,14}\oplus V_{3, 14}\oplus V_{3,16}=0 &&,\epsilon_4=-\frac14\\
\end{aligned}
\right.

去除中间变量，得到：

P_5\oplus K_{1,5}\oplus P_7\oplus K_{1,7}\oplus P_8 \oplus K_{1,8}\oplus K_{2,6}\oplus K_{3,6}\oplus K_{4, 6}\oplus U_{4,6}\\\oplus K_{4,14}\oplus U_{4,14}\oplus K_{3,14}\oplus K_{4,8}\oplus U_{4,8}\oplus K_{4,16}\oplus U_{4,16}=0

整理得：

P_5\oplus P_7\oplus P_8\oplus U_{4,6}\oplus U_{4,8}\oplus U_{4,14}\oplus U_{4,16}\oplus \sum k=0\\
\sum k=K_{1,5}\oplus K_{1,7} \oplus K_{1,8}\oplus K_{2,6}\oplus K_{3,6}\oplus K_{3,14}\oplus K_{4, 6}\oplus K_{4,8}\oplus K_{4,14}\oplus K_{4,16}

\sum k为一个固定的值，因此可由堆积引理计算出上述线性表达式（或仿射表达式，取决于\sum k的值）的偏置值为|\epsilon|=2\times (\frac14)^3=\frac1{32}。

最后一轮的处理

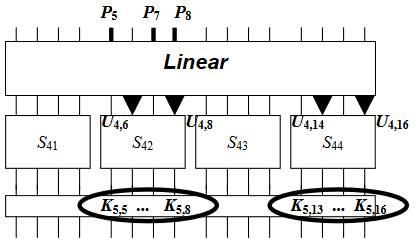
线性表达式仅到U_4一层为止，对于最后一轮的S盒，我们不再使用线性拟合，以防表达式过于复杂。由于只剩最后一层，我们可以从密文倒推回去。
由于是已知明文攻击，我们知道C_{1}\dots C_{16}的值，此时我们枚举K_{5,5}\dots K_{5,8},K_{5,13}\dots K_{5,16}的值，对于每个枚举，我们可以通过K_5\oplus C=V_4来计算出最后一轮的S盒的输出，并通过S盒的逆求得U_{5,5}\dots U_{5,8},U_{5,13}\dots U_{5,16}的值，我们将这些值代入线性表达式（或仿射表达式），如果表达式成立，那么给计数器的值加一，对每个已知明文对都做这样的操作，就能得到线性表达式实际成立的概率（或偏置值）。
例如，我们猜测K_{5,5}\dots K_{5,8}=1001,K_{5,13}\dots K_{5,16}=0010，且已知10000对明密文对，遍历这10000对明密文对，其中5021对使得线性表达式成立，那么可得偏置值为21/10000。
在所有对密钥的猜测中，我们选取偏置值和1/32最接近的，那么这个密钥就有很高的概率是真正的密钥。
实际测试中，10000对明密文对看上去有点少，可能产生错误的结果。可以适当提高明密文对的数量。

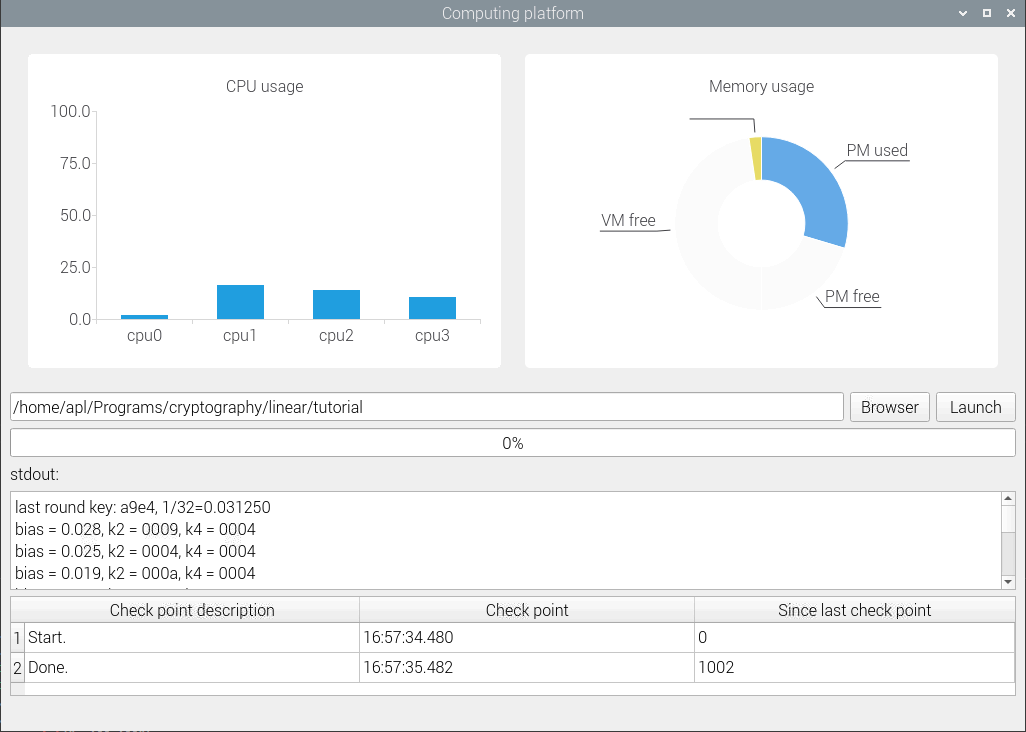
100000对明密文对仅需1002毫秒即可完成。测试机器为树莓派4b+，1GB内存。

参考资料

这份笔记的主要内容来源于A Tutorial on Linear and Differential Cryptanalysis by Howard M. Heys

1. A Tutorial on Linear and Differential Cryptanalysis by Howard M. Heys
2. 二维线性变换与实二阶矩阵

附录

1. 所有线性表达式成立的概率

probability.txt

2. 实验代码

使用C及C++完成。
tutorial.cpp
sspn.h